A number’s standard form, often known as scientific notation, is a method of representing big or tiny numbers in a succinct and practical style. It is written only between numbers 1 and 10 with power 10.
The “standard form” of a number in number theory often refers to expressing a particular number in a specific canonical or standard format. The particular standard form may vary depending on the context or type of number under consideration. It aims to simplify the expression of numerical values and make them easily understandable and comparable.
In this article, we will discuss the concept of standard form, notation of standard form, and way of writing decimal numbers in standard form, and merits and demerits of standard form. In addition, in this article example of standard form will be discussed.
Standard form of a number
The standard form of a number typically refers to expressing a number in a specific format that is widely recognized and used. In general, the standard form of a number is a representation that avoids unnecessary complexity and follows established conventions. In standard form, we use an exponent for representation.
Its other name is Scientific notation. Scientific notation gives the process of writing very large numbers or very small number using the number 1 to 10 and multiplying them with the power of 10. If the number is largest than one, we use positive power if the number is smallest than one, we use negative power of ten.
Notation of standard form
The representation of standard form is the place value of notation which complements the decimal number system.
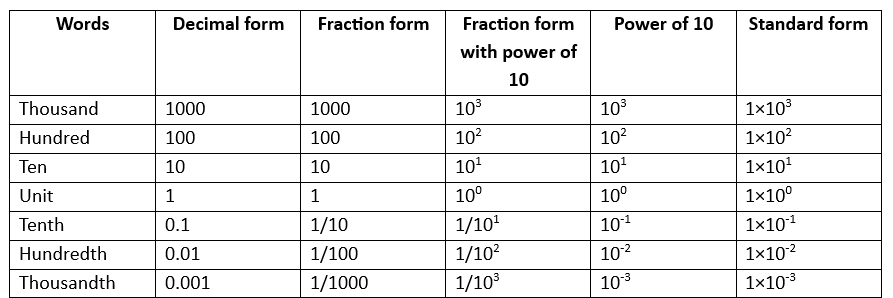
Way of writing decimal numbers in standard form
To write decimal numbers in standard form, multiply the number by a coefficient and a power of ten. The purpose is to portray the number more compactly and consistently, making it easier to read and compare to other numbers.
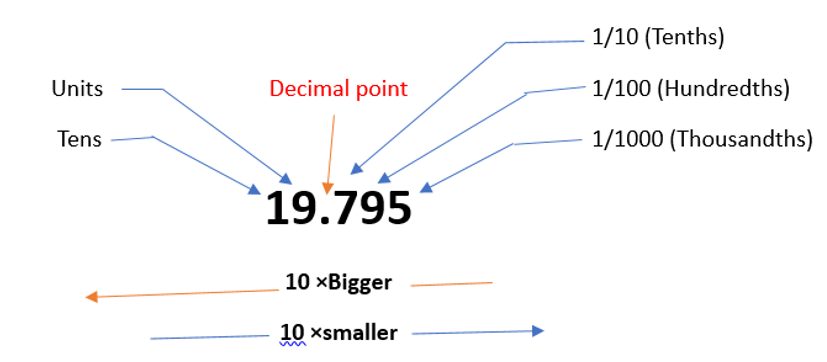
Step 1: Classify the Coefficient
It is clear that the left side of the decimal contains non-zero digits It must be a single non-zero digit (from 1 to 9).
Step 2: Count the Decimal Places
Count the number of decimal places the decimal point must shift to the right to convert the number to its original form (i.e., the number of places it must shift to the right to have a whole number).
Step 3: Write the Standard Form
Write the coefficient followed by the letter “x” (which represents multiplication) and the power of 10 as a superscript with the exponent being the number of decimal places counted in step 2.
You can also take assistance from a standard form converter for getting the results of converting numbers into standard notation.
Merits and demerits of standard form (Scientific Notation):
Merits and demerits depend on the contents we used. Here we discuss some merits and demerits of the standard form:
| Name | Merits | Name | Demerits |
| Compact Representation | The standard form allows us to represent extremely large or small numbers compactly and concisely. It is particularly useful when dealing with numbers that have many digits, making it easier to read and write. | Loss of Precision | When using standard form, some precision is sacrificed as numbers are rounded to a fixed number of significant digits. This rounding can lead to minor inaccuracies, especially in extensive calculations. |
| Comparisons and Approximations | The standard form facilitates easy comparisons between large and small numbers. It also makes it simpler to approximate values, which can be useful in various scientific and engineering applications. | Complexity in Basic Arithmetic | While standard form simplifies calculations involving large or small numbers, basic arithmetic operations like addition and subtraction can become more complicated due to converting numbers back and forth between standard form and regular form. |
| Clarity in Measurements | In scientific fields, the standard form is commonly used to express measurements with uncertainties, as it emphasizes the significant digits and the order of magnitude. | Ambiguity in Context | Sometimes, if not used carefully, the standard form can lead to ambiguity. For instance, 5.6 x 10^3 might be interpreted as 5600 or 56000, depending on the context. |
| Easy to calculate | Calculations involving very large or small numbers can be more manageable, as it reduces the chance of errors caused by working with numerous digits Using the standard form. | Limited Applicability | Standard form is most beneficial when dealing with quantities that differ significantly in magnitude. For moderate-sized numbers, the standard form may not offer significant advantages over regular decimal notation. |
| Scaling | It enables easy scaling of quantities without having to adjust all the digits. Multiplying or dividing by powers of 10 only requires shifting the decimal point, making the process straightforward. | Familiarity and Communication | In everyday life and certain fields where the standard form is not frequently used, expressing numbers in scientific notation may lead to confusion and miscommunication among people not familiar with this notation. |
How to find the standard form of a number?
Example 1
Convert 9,990,00 into standard form
Solution:
Step 1: Given the data
9, 990, 00
By rules, we can write them multiplication with a power of 10.
Step 2: Simplify
9, 990, 00 = 9.99 x 105
Example 2:
(1/2x) – x = -5.
Show the given equation in standard form.
Solution:
(1/2x) – x = -5
Step 1:
Multiplying with 2x on both sides,
1 – 2x (x)= -10x
Step 2:d
Simplify the equation
2x2 +10 x + 1 = 0
Therefore, the standard form of the given equation is 2x2 +10 x + 1 = 0.
Summary
In this article, we have discussed the concept of standard form, notation of standard form, and way of writing decimal numbers in standard form, and merits and demerits of standard form. Submitted by Mirza




